180nm CHIP of American Option Pricing Accelerator

In collaboration with 張家翔、莊詠翔、陳宥辰.
This is the final project of Integrated Circuit Design Lab (Spring 2022).
Will provide the github link after it is tidied up!

Introduction

Option is a certificate for future buying or selling of a certain merchandise. American option is a type of option that allows holders to exercise the option rights any time not later than the expiration date. Hence, every possible stock price fluctuation from now to the expiration date needs to be considered when conducting option pricing.

This design implements valuation of American call options using Monte-Carlo method. In terms of the random process equation of stock price fluctuations, several random option pricing paths are generated. By calculating the expected cashflows of all paths by means of regression, call option pricing is performed.

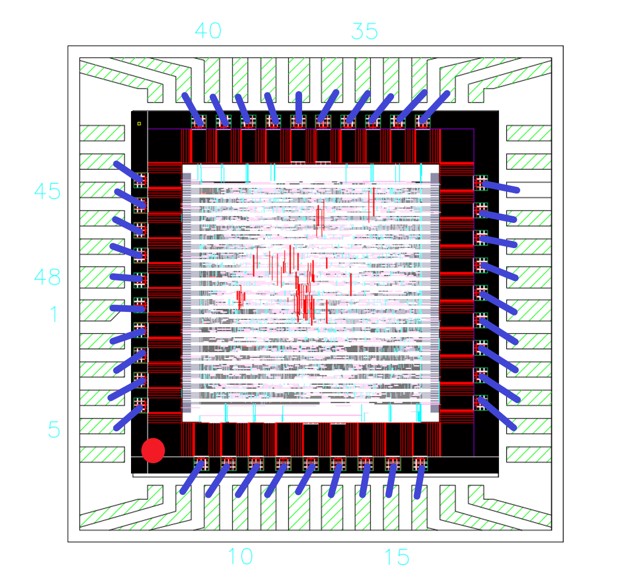
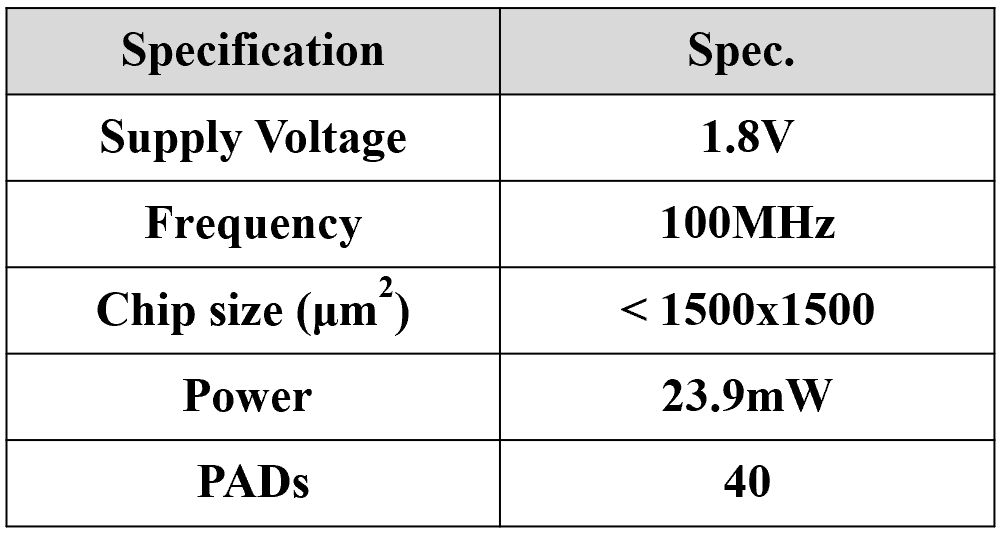
The chip is fabricated using 180nm UMC technology. Its summary is provided as follows.

==================== 😎 我是分隔線 😎 tl;dr 😎 ====================

Inplementation Details

Overview

We begin by utilizing the Sobol random number generator to produce a 16-bit random variable. This variable is then input into the Inverse Cumulative Distribution Function (ICDF) to generate a Gaussian distributed signal 𝜀. By incorporating w, q, S0, and the generated 𝜀 into the daily stock price generator (Path Generator), we can generate daily stock prices (Paths) with randomness. Here, w and q are constants related to the stock price and volatility, and S0 is the current stock price. Subsequently, the daily stock prices and the strike price (K) of the American-style option are input into the Monte Carlo Core of the second part, resulting in a Cash Flow Matrix. Averaging the columns of this Cash Flow Matrix yields the pricing for the American-style option.

The overall architecture of this chip design is illustrated in Figure 1 and can be divided into two main parts. The first part generates daily random stock prices (Sobol RNG, ICDF, Path Generator), while the second part focuses on American-style option pricing (Pricing). The subsequent sections will provide a sequential explanation of these components.

Figure 1: Chip Overall Architecture

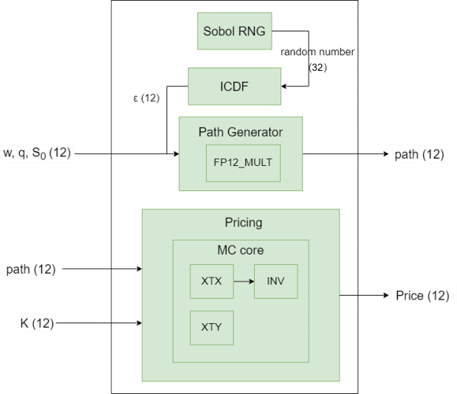
Principle and Architecture of Generating Random Stock Prices

During the generation of each price path, it is necessary to employ a random variable ε to simulate the stochastic nature of price fluctuations. Figure 2 below depicts the generation process of ε. In this experiment, Sobol low-discrepancy sequence is utilized as the foundation for generating random variables. These variables are then transformed into Gaussian random variables using the inverse of the cumulative distribution function of the Gaussian distribution, referred to as the Inverse Cumulative Distribution Function (ICDF). This conversion serves as a crucial step in generating the required price paths.

Figure 2: Process of Generating Random Variable ε

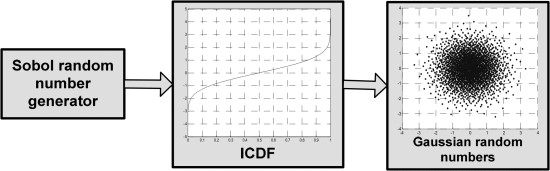
The Sobol low-discrepancy sequence is a form of quasi-random numbers. This approach provides a systematic way to generate the required sequence. While strictly speaking, the generated numbers are not entirely random, they offer a higher generation speed compared to true random numbers. Moreover, it has been demonstrated that Sobol sequences exhibit results similar to true random numbers in Monte Carlo simulations. This characteristic has led to their widespread adoption in financial and quantitative analysis.

The choice to use quasi-random numbers, such as Sobol sequences, rather than typical pseudo-random numbers, is aimed at addressing the issue of uneven distribution in multi-dimensional spaces. This phenomenon is demonstrated in Figure 3, where pseudo-random numbers are generated using the Mersenne Twister random number generator. Figure 4 illustrates the partitioning of the distribution range into small 20x20 grids. The discrepancy between the actual occurrence rate at the midpoint of each grid and the expected uniform distribution rate is calculated. The resulting visualization indicates a noticeable clustering effect on the right-hand side, highlighting the improvement brought about by using quasi-random numbers.

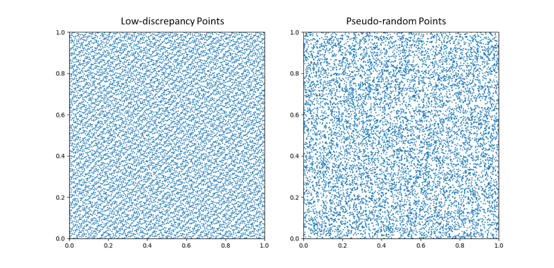
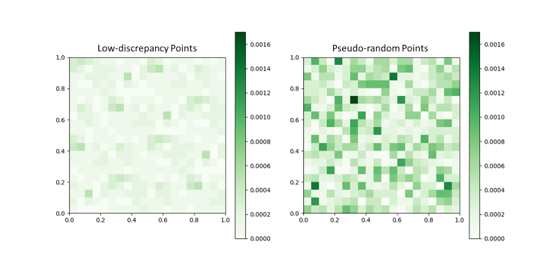
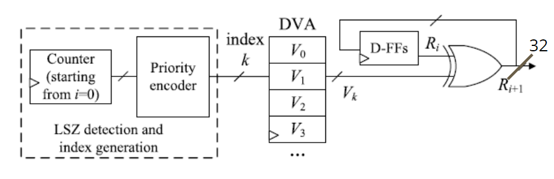
Figure 5 depicts the hardware architecture details of the Sobol random number generator. The generation algorithm primarily employs the Gray code recursive approach proposed by Antonov-Saleev (1979). It begins by using a counter to generate an index starting from 0. This 32-bit index is then fed into a Priority Encoder to detect the position of the Least Significant Zero (LSZ), i.e., the lowest binary digit that is 0.

Based on the position of LSZ, the current random number R_i is XORed with the corresponding Direction Vector. This operation results in the generation of the next random number R_i+1. The Direction Vector is computed through recursive operations using the coefficients of primitive polynomials. In our implementation, we pre-computed the entire set of Direction Vectors using a Python program and stored them in a Direction Vector Array (DVA) within the chip. This simplifies the calculation process and enhances computational speed.

Figure 5: Architecture of Sobol Random Number Generator

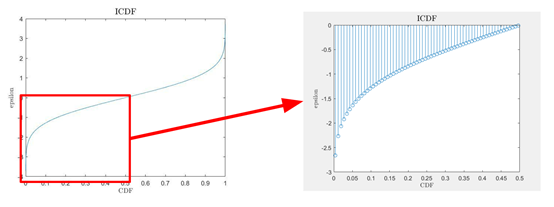
To convert the random numbers generated by the Sobol random number generator into a Gaussian distribution, it is necessary to transform them through the Inverse Cumulative Distribution Function (ICDF) of the Gaussian distribution. Due to limitations in the number of chip pins, performing this transformation externally on the chip is impractical and time-consuming. However, the ICDF of the Gaussian distribution itself is not analytically solvable, so we use a first-order linear segmented approximation to simulate the original function graph.

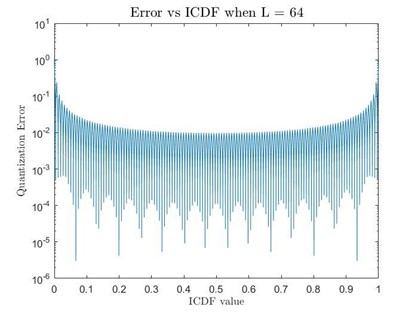
The approach involves solving for 64 points on the original function and storing these values on the chip for quantized table lookup. Since the ICDF is symmetric around x=0.5, the graph of the interval x=0~0.5 can be used as a reference, as shown in Figure 6. This method achieves Gaussian distribution transformation on the chip, with an average error rate of 1.27%, as shown in Figure 7.

Translation unfinished, See the report below...

Tape-out Report (In Chinese)

Reference

[1] Tian, Xiang, and Khaled Benkrid. “American option pricing on reconfigurable hardware using least-squares monte carlo method.” 2009 International Conference on Field-Programmable Technology. IEEE, 2009.

[2] Liu, Siting, and Jie Han. “Toward energy-efficient stochastic circuits using parallel Sobol sequences.” IEEE Transactions on Very Large Scale Integration (VLSI) Systems 26.7 (2018): 1326-1339.

[3] Dikshit, Akriti, Gayathri Prasad, and Maran Ponnambalam. “Design and Analysis of Sobol Sequence Generator using gray code parallelization.” 2021 2nd Global Conference for Advancement in Technology (GCAT). IEEE, 2021.